Patent application title: METHOD FOR DETERMINING PROPERTIES OF A HYDROCARBON RESERVOIR FORMATION AND PRODUCED FLUIDS IN THE PROCESS OF PRODUCTION
Inventors:
Arkady Yurievich Segal (Moscow, RU)
Assignees:
SCHLUMBERGER TECHNOLOGY CORPORATION
IPC8 Class: AE21B4400FI
USPC Class:
16625015
Class name: Processes with indicating, testing, measuring or locating automatic control for production
Publication date: 2014-03-06
Patent application number: 20140060822
Abstract:
An acoustic signal is recorded at least once, the signal being a response
of a wellbore-reservoir system onto acoustic impulses of pressure. A
source of the pressure impulses is an electric submersible pump located
inside the wellbore. The acoustic signal is recorded at least once by at
least one sensor placed in a bottomhole chamber of the wellbore, the
sensor measuring at least one physical parameter of the
wellbore-reservoir system, which characterizes a process of propagation
of the acoustic signal in the wellbore. A mathematical model of
propagation of acoustic signals in the bottomhole chamber is created and
data obtained by means of modeling are compared with data obtained by
means of registering of the acoustic signals. Parameters of the reservoir
formation in the mathematical model are adjusted in order to provide for
consistency of at least one quantitative physical characteristic of the
wellbore-reservoir system obtained by means of modeling with the same
quantitative physical characteristic obtained by registration, and
properties of the reservoir and of the produced fluids are determined as
parameters providing for consistency.Claims:
1. A method for determining properties of a hydrocarbon reservoir
formation and of produced fluids, comprising: registering an acoustic
signal at least once, the acoustic signal being a response of a
wellbore-reservoir system onto acoustic impulses of pressure whose source
is an electric submersible pump located inside the wellbore, and the
acoustic signal is registered by at least one sensor placed in a
bottomhole chamber of the wellbore and measuring at least one qualitative
physical characteristic of the wellbore-reservoir system, which
characterizes a process of propagation of the acoustic signal in the
wellbore; creating a mathematical model of propagation of the acoustic
impulses of pressure in the bottomhole chamber; comparing data obtained
by means of modeling with data obtained by means of registration of the
acoustic signal, which is the response of the wellbore-reservoir system;
adjusting parameters of the reservoir in the mathematical model in order
to provide for consistency of at least one qualitative physical
characteristic of the wellbore-reservoir system obtained by means of
modeling with the same qualitative physical characteristic obtained by
means of registration, and determining properties of the reservoir
formation and the produced fluids as parameters providing for
consistency.
2. The method of claim 1, wherein the at least one qualitative physical characteristic of the wellbore-reservoir system is selected from the group consisting of pressure, a pressure derivative with respect to time, a component of velocity of the fluid, and a component of acceleration of the fluid.
3. The method of claim 1, wherein two groups of sensors located close to each other are used, at least one sensor in the first group measures pressure or a derivative of pressure with respect to time or a combination thereof, in the second group at least one sensor measures velocity or acceleration of a fluid in the direction of a wellbore axis in a place of measurement, the ratio of the spectrum of the first measured physical qualitative characteristic to the spectrum of the second measured physical quantitative characteristic is determined, the said ratio of the spectrum of the first measured physical qualitative characteristic to the spectrum of the second measured physical quantitative characteristic is used as input data for calculating a response function of the reservoir using the model of propagation of acoustic impulses in the bottomhole chamber of the wellbore, a set of response functions of the reservoir associated with a certain geometry of the reservoir formation and parameters of the medium of the formation is used for adjusting parameters of the reservoir formation in the mathematical model.
4. The method of claim 3, wherein determining the ratio of the spectrum of the first physical quantitative characteristic to the spectrum of the second measured physical quantitative characteristic, the spectrum of the first measured physical quantitative characteristic is calculated for the first group of sensors and the spectrum of the second measured qualitative characteristic is calculated for the second group of sensors.
5. The method of claim 4, wherein the calculation of the spectrum of the measured physical quantitative characteristic comprises processing the registered acoustic signal which includes presenting the signal as a linear combination of functions parameterized by a spectral parameter, with coefficients of a linear combination of the said spectrum.
6. The method of claim 5, wherein the processing of the registered acoustic signal is made with the use of the discrete Fourier transform.
7. The method of claim 6, wherein a preliminary processing of the registered acoustic signal is carried out.
8. The method of claim 7, wherein the preliminary processing of the registered acoustic signal comprises exclusion of trends and removal of noises.
9. The method of claim 3, wherein the ratio of the spectrum of the first measured physical quantitative characteristic to the spectrum of the second measured physical quantitative characteristic is calculated as a linear filter.
10. The method of claim 1, wherein if the acoustic signal is registered more than once, a spectrum of the physical quantitative characteristic measured by the sensor is calculated for each measurement, changes in at least one parameter of the mathematical model are determined by f comparing the resultant changes in the spectra with the changes in parameters of the model.
11. The method of claim 10, wherein the calculation of the spectrum of the measured physical quantitative characteristic comprises processing of the registered acoustic signal; presenting the signal as a linear combination of functions parametrized by a spectral parameter, with coefficients of the linear combination constituting the said spectrum.
12. The method of claim 1, wherein a rotation velocity of a rotor of the electric submersible pump is varied at least once by varying a control input signal of the electric submersible pump, the spectrum of at least one measured quantitative physical characteristic is determined at a discrete set of frequencies on which amplitudes of the spectrum of the submersible pump have local maxima.
13. The method of claim 12, wherein the rotation velocity of the rotor of the electric submersible pump is varied with the use of a variable speed drive.
14. The method of claim 12, wherein variations in the rotation velocity of the rotor comprises frequency modulation of the rotation velocity of the rotor by a modulating frequency.
15. The method of claim 12, wherein the rotation velocity of the rotor of the electric submersible pump is varied several times with a set of different modulating parameters in such a way that spectral maxima of the rotation velocity of the rotor cover a frequency range.
16. The method of claim 15, wherein the variation in the rotation velocity of the rotor comprises frequency modulating in which a variation in the modulating parameter results in the spectral maxima covering the range: (vsh-nvmod,vsh+nvmod), where vsh is the rotation velocity of the rotor of the electric submersible pump, vmod is the modulating parameter, n=1, 2 . . . .
17. The method of claim 1, wherein pressure or its derivative with respect to time, or a combination thereof, is measured by at least one sensor, phase velocity of the fluid filling the bottomhole chamber of the wellbore is determined by means of correlating resonance and anti-resonance frequencies of at least one quantitative characteristic to the corresponding frequencies of the mathematical model, and a volume ratio of a gas is determined, which includes the ratio of a volume occupied by the gas to a total volume of the fluid, by means of correlating phase velocity of propagation of the pressure impulses determined at a given pressure with a phase velocity predicted with the use of the model.
18. The method of claim 17, wherein a change in the volume ratio of the gas is determined qualitatively by means of observing simultaneous decrease or increase of resonance or anti-resonance frequencies.
19. The method of claim 1, wherein the acoustic signals registered by the sensors measuring at least one quantitative physical characteristic of the wellbore-reservoir system are subjected to processing in the wellbore in such a way that information about quantitative or qualitative behavior of the physical quantitative characteristics is developed by means of such processing and either is transmitted to the surface with the use of a telemetry link or is stored in a memory for subsequent readout in the future.
Description:
CROSS-REFERENCE TO RELATED APPLICATION
[0001] This application claims priority to Russian Patent Application No. 2012137226 filed Sep. 3, 2012, which is incorporated herein by reference in its entirety.
FIELD
[0002] This subject disclosure relates to monitoring of properties of a hydrocarbon reservoir formation and properties of produced fluids in the process of production, in particular, in the process of artificial lift.
SUMMARY
[0003] Artificial lift is an operation aimed at enhancement of production of hydrocarbons from a reservoir by means of creating a negative differential pressure between the reservoir and the wellbore, and then--between the bottomhole zone of the well and the surface in such a way as to first induce inflow of the fluid from the reservoir into the well and then to force out these fluids to the surface. This is a universally accepted method of production, implemented, in particular, by means of installing an electric submersible pump (ESP) inside a producing well. The electric submersible pump comprises a series of several centrifugal pumps, a separator, an electric motor and a power cable for supplying power to the motor. The power system may include the Variable Speed Drive that is capable of regulating the incoming electric signal and thus to vary performance characteristics of the electric submersible pump if needed.
[0004] During production, it is important to estimate variations in formation conditions (for example, pressure, permeability in the near-wellbore zone of the formation and local reductions of permeability) and changes in properties of wellbore fluids (for example, contents of different phases in them) and to promptly adjust parameters of the electric submersible pump and the system installed at the surface with the purpose to create the optimal production regime, to exclude equipment failures, and to acquire additional data for engineering models.
[0005] From the prior art, methods are known for acquiring information on properties of hydrocarbon reservoirs, which include harmonic tests (see, for example, Hollaender, F., Hammond P. S. and Gringarten, A., Harmonic Testing for Continuous Well and Reservoir Monitoring, SPE 77692, 2002), which envisage exerting a load onto the reservoir that is associated with cyclic variation of flow rate of the fluid, with varying the period of the cycle within a certain range, with the purpose to determine the "response function" of the formation that is the ratio of pressure in the frequency domain to flow rate in the frequency domain (from now on, mentioning of any quantity "in the frequency domain" means a reference to complex coefficients of the Fourier transform of this quantity parameterized by frequency) at the intersection of the reservoir formation and the wellbore. From the viewpoint of the acoustics, the response function coincides with lumped hydraulic impedance of the formation in the zone of its adjoining to the well. If the flow rate is known, the response function makes it possible to calculate pressure in the frequency domain. Analytical models of the response function were considered for various "well-reservoir" configurations: a linear source, a well with consideration of compressibility of the wellbore and a zone of local permeability reduction in an infinite homogeneous reservoir layer, a well with a hydraulically fractured formation, dual porosity reservoirs, or composite reservoirs with consideration of compressibility of the wellbore and the zone of local permeability reduction.
[0006] Periods of cycles of harmonic tests are correlated to the needed depth of investigation of the reservoir and are varied from 0.1 sec to several months; thus, the estimated frequency range of the response function does not exceed 10 Hz. The corresponding changes in the flow rate should be made with the use of a special device for varying the flow rate, and this complicates the well design.
[0007] As distinct from the standard harmonic tests, the suggested method pertains to a higher frequency range (10-100 Hz) and estimates the response function of the formation indirectly, through its hydraulic resistance at the measurement point, for example, at the intake of the electric submersible pump. The transition to another frequency range makes it possible to investigate formation properties at a distance from the well but also to characterize parameters of the near-wellbore zone and to obtain better-property characteristics of the formation at the interface of the reservoir and the well. It also makes it possible to base data interpretation on phenomena that are unavailable in the case of lower frequencies, for example, on frequencies and decay rates of resonance modes in the zone below the pump.
[0008] In accordance with the suggested method, an acoustic signal is recorded at least once, the acoustic signal being a response of a wellbore-reservoir system onto acoustic impulses of pressure whose source is an electric submersible pump installed inside the wellbore. The acoustic signal is acquired by at least one sensor, which is located in a bottomhole chamber of the well and measures at least one quantitative physical characteristic of the wellbore-reservoir system characterizing a process of propagation of the acoustic signal in the wellbore. A mathematical model of propagation of acoustic impulses in the bottomhole chamber is created; data obtained by means of modeling are compared with data obtained by means of acquisition of the acoustic signal that is the response of the wellbore-reservoir system. Parameters of the reservoir formation in the mathematical model are adjusted in order to provide for consistency of at least one quantitative physical characteristic of the wellbore-formation system obtained through modeling to the same quantitative physical characteristic obtained by means of recording, and properties of the formation and the produced fluids are determined as parameters providing for the said consistency.
[0009] The at least one quantitative physical characteristic of the wellbore-reservoir system is selected from a group consisting of pressure, a pressure derivative with respect to time, a component of velocity of the fluid, a component of acceleration of the fluid, or a combination thereof.
[0010] In accordance with an embodiment, two groups of sensors are used for registration of the acoustic signal, which are located close to each other. In the first group, at least one sensor measures pressure or pressure derivative with respect to time, or a combination thereof; in the second group at least one sensor measures a fluid velocity or acceleration in the direction of a wellbore axis at a place of measurement. A ratio of a spectrum of the first measured physical quantitative characteristic to a spectrum of the second measured physical quantitative characteristic is determined, the said ratio of the spectrum of the first measured physical quantitative characteristic to the spectrum of the second measured physical quantitative characteristic is used as input data for calculating the response function of the formation using the mathematical model of propagation of the acoustic impulse in the bottomhole chamber of the well. The set of response functions of the formation obtained from modeling, that is associated with geometry of the formation and parameters of the formation medium, is used for adjusting parameters of the reservoir formation in the mathematical model.
[0011] Determining the ratio of the spectrum of the first measured physical quantitative characteristic to the spectrum of the second measured physical quantitative characteristic, the spectrum of the first measured physical quantitative characteristic for the first group of sensors and the spectrum of the second physical quantitative characteristic for the second group of sensors are calculated. Calculation of a spectrum of the measured physical quantitative characteristic includes processing of the recorded acoustic signal which includes presenting the signal as a linear combination of functions parameterized by a spectral parameter, with coefficients of this linear combination that constitute the said spectrum.
[0012] In particular, determination of the spectrum of the recorded acoustic signal may be made with the use of the discrete Fourier transform.
[0013] The registered acoustic signal may be subjected to preprocessing that may include, for example, exclusion of trends and removal of noises.
[0014] The ratio of the spectrum of the first measured physical quantitative characteristic to the spectrum of the second measured physical quantitative characteristic may be computed as a linear filter.
[0015] In the event that the acoustic signal is recorded more than once, spectrum of the physical quantitative characteristic measured by the sensor is calculated for each measurement, and variations of at least one parameter of the physical model are determined by means of comparing the resultant variations of the spectra with variations of parameters of the model.
[0016] In accordance with another embodiment, a rotation velocity of a rotor of the electric submersible pump is varied at least once by means of varying a control input signal of the electric submersible pump, spectrum of at least one quantitative physical characteristic measured by sensors is determined, with a discrete set of frequencies at which amplitudes of the spectrum of the electric submersible pump have local maxima. The rotation velocity of the rotor of the electric submersible pump may be varied with the use of a Variable Speed Drive.
[0017] Varying the rotation velocity of the rotor may include a frequency modulation of the rotation velocity of the rotor by a modulating frequency.
[0018] The rotation velocity of the rotor of the electric submersible pump may be modified several times with a set of various modulating parameters in such a way that spectral maxima of the rotation velocity of the rotor would cover a certain frequency range.
[0019] In particular, a variation of the rotation velocity of the rotor may include frequency modulation in which variation of the modulating parameter results in spectral maxima covering the range
(vsh-nvmod,vsh+nvmod),
[0020] where vsh is the rotational velocity of the rotor of the electric submersible pump,
[0021] vmod is a modulating parameter,
[0022] n=1, 2 . . . .
[0023] In accordance with yet another embodiment, at least one sensor measures pressure or its derivative with respect to time, or a combination thereof, and a phase velocity of a fluid filling the bottomhole chamber of the well is determined by means of correlating resonance and anti-resonance frequencies of at least one quantitative characteristic with corresponding frequencies of the mathematical model. A volume ratio of a gas is determined, which is the ratio of a volume occupied by the gas to an entire volume of the fluid, by means of correlating the phase velocity determined at the given pressure with the phase velocity predicted by the model.
[0024] A change in the volume ratio of gas may be determined qualitatively by observing simultaneous decrease or increase of resonance or antiresonance frequencies.
[0025] The acoustic signals registered by the sensors, which measure at least one quantitative physical characteristic of the well-reservoir system, may be subjected to processing in the well in such a way that information on quantitative or qualitative behavior of the physical quantitative characteristics is generated by means of such processing and is transmitted to the surface with the use of a telemetry data link or is stored in the memory for reading-out in the future.
BRIEF DESCRIPTION OF DRAWINGS
[0026] The subject disclosure is further described in the detailed description which follows, in reference to the noted plurality of drawings by way of non-limiting examples of the subject disclosure, in which like reference numerals represent similar parts throughout the several views of the drawings, and wherein:
[0027] FIG. 1 shows an example of frequency modulation of rotation velocity of the rotor;
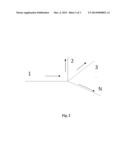
[0028] FIG. 2 illustrates the equation of mass conservation at the junction of several segments; and
[0029] FIG. 3 shows an example of hydraulic impedance at the intake of the electric submersible pump calculated in the model of a transmission line for the geometry illustrated in the left.
DETAILED DESCRIPTION
[0030] The particulars shown herein are by way of example and for purposes of illustrative discussion of the examples of the subject disclosure only and are presented in the cause of providing what is believed to be the most useful and readily understood description of the principles and conceptual aspects of the subject disclosure. In this regard, no attempt is made to show structural details in more detail than is necessary, the description taken with the drawings making apparent to those skilled in the art how the several forms of the subject disclosure may be embodied in practice. Furthermore, like reference numbers and designations in the various drawings indicate like elements.
[0031] The subject disclosure is based on utilizing the electric submersible pump as a source of pressure oscillations that fill the wellbore space with acoustic energy; taking into consideration that the section of the wellbore located below the electric submersible pump is a perfectly isolated volume, which makes it suitable for acoustic tests.
[0032] Interpretation of these oscillations makes it possible to characterize properties of the reservoir formation or of the wellbore fluid based, in particular, on the dynamic response of pressure.
[0033] It was established that a possibility exists to estimate some properties of the reservoir formation or the wellbore fluid by means of directing the pressure impulse toward the lower part of the wellbore and interpreting the response of the system, which is sensitive to hydraulic communication of the wellbore and the reservoir and to compressibility coefficients of wellbore fluids, at that the latter are indicators of contents of different phases in the fluid. For creating such pressure oscillations, an electric submersible pump may be used. Application of a downhole pressure sensor or a sensor for measurement of flow rate oscillations (for example, a single-component geophone), or of both sensors makes it possible to record the response of the system. The sensors are placed in the bottomhole chamber of the wellbore; the notion "bottomhole chamber" means a hydraulically connected space below the electric submersible pump and may include a group of segments of the wellbore that are either hydraulically separated from the medium surrounding the wellbore or connected with this medium, and may comprise at least one reservoir formation intersecting by the wellbore, and may also comprise a space below the packer if the latter is present.
[0034] A mathematical model is created of propagation of a pressure impulse in the reservoir formation adjoining the wellbore zone located below the electric submersible pump; the models' parameters may be adjusted in such a way that results of modeling would match the measured data. The model should include a set of parameters of the reservoir formation, for example, the product of formation permeability by formation height, local reduction of permeability in the near-wellbore zone, mean radius of the permeability reduction zone, and of parameters of the fluid, for example, density, viscosity and volume ratio of gas.
[0035] The electric submersible pump is a type of centrifugal pump in which rotary movement of a profiled impeller in combination with a shaped pump shell, or volute, imparts a centrifugal force for expelling the fluid from the pump. The fluid enters into the pump and is sucked into the vane space or into the center of the impeller, and the fluid is pushed out via the vanes (blades) under the action of the centrifugal force created by the rotative action of the impeller. The fluid is then forced out into the outer circuit of the pump and goes out from the pump discharge.
[0036] Several impeller stages may be installed on the shaft, and a multistage centrifugal pump is thus created, which may be used in artificial lift. (See, for example, http://belpumps.by/inoxpa-nasos-ms.html).
[0037] The centrifugal pump performs work over the fluid, imparting the force by means of accelerating the fluid to a certain velocity and relocating it from the state of low pressure (at the pump suction) to the state of high pressure (at the pump discharge). The work is performed over the fluid by means of rotating the impeller fixed on the shaft and connected to the power source--an electric motor, diesel engine, etc.
[0038] As the shaft rotates, the fluid enters into the "vane space" of the impeller (the zone closest to the shaft) and exits through the vanes located at the brim or at the external diameter. The fluid exits from the blade edge with a certain velocity and under certain pressure and is directed from the outer diameter of the impeller through the diffuser and returns to the outer diameter (the "vane space") of the next impeller or to the pump discharge. The diffuser is stationary and has blades, which create a pass channel for altering the movement direction of the fluid.
[0039] Thus, it follows from the operation principle of the centrifugal pump itself that two fundamental frequencies exist that characterize operation of the pump: the rotation frequency of the impeller ("shaft frequency") and the frequency of the "inter-vane channel" that includes the rotation frequency of the impeller times the number of vanes. These frequencies manifest themselves in the form of peaks in the spectrum of pressure oscillations created by the pump. In view of the fact that time dependence of rotation speed of the shaft may not have a perfect sine curve, and the fact that pressure response to rotation of the rotor may be non-linear, a spectrum of pressure response also contains harmonic components of the fundamental frequencies ("the harmonics").
[0040] Thus, the electric submersible pump is capable of generating strong acoustic signals on a multitude of "tones" proportional to the rotation frequency of the shaft. A considerable amount of wide-band noises of lower amplitudes also exists. While generation of the signal inside the pump may be complicated and be a non-linear process, its subsequent propagation inside the wellbore fluid and the reservoir formation can be adequately described with the use of linear approximation. The signal can then be considered as a sum of harmonic modes in which each frequency component propagates independently, this approach is to a considerable extent similar to a realization of the Fourier transform and the transition to qualitative parameters in the frequency domain. Spatial profile of each mode can be computed within the framework of a mathematical model of the type of model of a transmission line, which considers the wellbore as an assemblage of one-dimensional segments maintaining tube waves directed upward and downward, and considers the reservoir formation as a zero-dimensional element of lumped impedance determining the response of the formation onto variations in pressure/flow rate.
[0041] It is important to have an opportunity to vary frequencies of the spectral maxima in the spectrum of the pump pressure with the purpose of providing for the possibility of scanning a certain frequency range. This can be done in a natural way by means of modulating the characteristics of rotation of the pump. One of the possibilities is utilization of a variable speed drive which is the control system of the electric drive that is capable of regulating the input electric signal and, by means of this, the rotation frequency of the pump shaft.
[0042] The Variable Speed Drive is a device for converting the input energy of alternate current with a fixed frequency into the output energy of alternate current with a variable frequency. To do this, the variable speed drive converts the input signal of alternate current into a signal of direct current, which is maintained at the preset level in the direct current bus. At the output of this bus, with the use of the inverter, direct current is converted back into the energy of alternate current of the frequency.
[0043] A slow harmonic variation of rotation frequency of the shaft vsh with a frequency vmod concerts the original harmonic signal into a sequence of harmonic signals with frequencies vsh±nvmod, n=0, 1, 2, . . . . Thus, having concentrated on the zone n=1, it is possible to cover the range vsh-vmod<vsh+vmod by means of varying the modulating frequency vmod.
sin(2πv0t+A sin(2πv1t))→v0±nv1,n=0,1,2, (1)
[0044] This is illustrated in FIG. 1 where the upper diagram pertains to the time domain and the lower one--to the frequency domain. The dashed lines characterize the harmonic signal with the frequency v0=60 Hz. The solid lines characterize its frequency-modulated analog v1=10 Hz.
[0045] In this case, the modulated signal is characterized by a single parameter v1 and by a discrete frequency spectrum. Other modulating sequences are possible, which are characterized by a more general spectrum with its set of fundamental frequencies. We name the modulating sequence characterized by a specific spectrum the modulating cycle, while frequencies of the corresponding spectral maxima are named focus frequencies.
[0046] Each modulating cycle is realized during some period of time in order to obtain, with a sufficient accuracy, the time-independent spectrum of the response of the system on a multitude of focus frequencies or within a preset frequency range; then the modulating parameters are varied with the purpose of varying the focus frequencies. The said procedure is iterated many times (if this is possible from the operational viewpoint) in order to cover as many focus frequencies in the range under consideration.
[0047] It is not necessary to generate strictly harmonic impulses and vary the frequency in time; the same response function will be obtained by means of generating an arbitrary impulse subsequently obtaining the response function as the ratio of the pressure and flow rate subjected to the Fourier transform. As an alternative of the Fourier transform, for specialists in signal processing, a number of algorithms for evaluation of a spectrum are known, including procedures of clearing a signal from noises. By virtue of a relatively high dominant frequency (either the rotation frequency of the shaft or the frequency of the vane channel), a typical signal recording period lasting for several seconds comprises hundreds or thousands of oscillation cycles, this is quite sufficient for estimating the spectrum with the use of the discrete Fourier transform, thus, duly normalized values of spectral density will approximate, with a high accuracy value, the theoretical values obtained by means of the Laplace transform or the Fourier transform.
[0048] Within the transmission-line approach, a model is created of propagation of an impulse in the wellbore system connected with at least one reservoir formation. A model can be used if a wave length of excitations exceeds the usual size of joints between segments. If a length of tube waves becomes commensurable with or less than the height of the reservoir formation, a more sophisticated model becomes necessary for processing the "wellbore-reservoir" system, which can be developed if needed. In addition, a relatively small size of the bottomhole chamber opens the possibility of direct numerical modeling with the use of one of the modern modeling means. An example of utilizing this principle for a hydraulically fractured well is presented in T. W. Patzek, A. De, A Lossy Transmission Line Model of Hydrofractured Well Dynamics, Journal of Petroleum Science and Engineering 25 (2000), 59-77, though we need a more general model considering a more complex relationship of principal qualitative characteristics versus frequency. In the general case, a one-dimensional transmission line is an assemblage of one-dimensional segments and zero-dimensional elements of lumped impedance. One-dimensional segments maintain two wave excitations propagating in opposite directions and written with the use of two quantitative characteristics: pressure p (x, t) and velocity v (x, t) in the form:
p(x,t)=p.sub.→(x,t)+p.sub.(x,t)
v(x,t)=v.sub.→(x,t)+v.sub.(x,t) (2)
or having conducted the Laplace transform with respect to t and transitioning to the complex frequency domain:
A ~ ( s ) = ∫ 0 ∞ A ( t ) - st t ( 3 ) p ~ ( x , s ) = p ~ -> ( x , s ) + p ~ ( x , s ) v ~ ( x , s ) = v ~ -> ( x , s ) + v ~ ( x , s ) ( 4 ) ##EQU00001##
Where
[0049] {tilde over (p)}.sub.→(x,s)=P.sub.→(s)exp(-γ(s)x),{tilde over (p)}.sub.(x,s)=P.sub.(s)exp(γ(s)x)
{tilde over (v)}.sub.→(x,s)=V.sub.→(s)exp(-γ(s)x),{tilde over (v)}.sub.(x,s)=V.sub.(s)exp(γ(s)x) (5)
with the complex-valued propagation constant γ (s) and amplitudes P (s), V (s).
[0050] The point-by-point ratio of the amplitude of the leftward-propagating wave to that of the rightward-propagating wave is the reflection coefficient, for example, for pressure
R ( x , s ) ≡ p ~ → ( x , s ) p ~ ( x , s ) = P ( s ) P → ( s ) exp ( 2 γ ( s ) x ) ( 6 ) ##EQU00002##
We obtain
R ( x 2 , s ) R ( x 1 , s ) = exp ( 2 γ ( s ) ( x 2 - x 1 ) ) ( 7 ) ##EQU00003##
[0051] Amplitudes of pressure and velocity are not independent but are interrelated by means of a complex-valued frequency-dependent wave impedance:
P.sub.→(s)=Zc(s)V.sub.→(s)
P.sub.(s)=-Zc(s)V.sub.(s) (8)
[0052] The real part of Zc (s) is the relationship between pressure and velocity of the "friction" type and signals pressure loss due to emission from the source or due to friction, while the imaginary part is responsible for capacitive resistance, inertia and other effects associated with accumulation of energy.
[0053] Equation (8) reduces the number of independent complex constants in Equation (5) to two: P.sub.→(s), P.sub.(s), which reflect complex amplitudes of waves directed rightward and leftward.
[0054] The point-by-point impedance is the ratio of pressure and velocity at a particular point:
Z ( x , s ) ≡ p ( x , s ) v ( x , s ) = Z c ( s ) exp ( - γ ( s ) x ) + r ( s ) exp ( γ ( s ) x ) exp ( - γ ( s ) x ) - r ( s ) exp ( γ ( s ) x ) , r ( s ) = P ( s ) P → ( s ) ( 9 ) ##EQU00004##
[0055] In contrast to Zc (s), which depends on local properties of the line, Z (x, s) depends on the entire geometry of the system trough r(s). Boundary conditions can be reformulated in terms of point-by-point resistance. For example, a closed boundary assumes v=0, and for this reason, Z (xend, s)=∞, while the condition for an open boundary p=0 is equivalent to Z (xend, s)=0. Acoustic emission through the boundary will yield some frequency-dependent impedance p (xend, s)=Zc (xend, s)v(xend, s):
R ( x , s ) ≡ Z ( x , s ) - Z c ( s ) Z ( x , s ) + Z c ( s ) ( 10 ) ##EQU00005##
[0056] Using (8), (9), it is possible to express point-by-point overall impedance at a point through point-by-point impedance at another point:
Z ( x 1 , s ) = Z c ( s ) 1 + exp ( 2 γ ( s ) ( x 1 - x 2 ) ) R ( x 2 , s ) 1 - exp ( 2 γ ( s ) ( x 1 - x 2 ) ) R ( x 2 , s ) , R ( x 2 , s ) ≡ Z ( x 2 , s ) - Z c ( s ) Z ( x 2 , s ) + Z c ( s ) ( 11 ) ##EQU00006##
which is the transfer equation of impedance. This relationship for resistances does not depend on a particular solution. If the target frequency range is such that wave lengths of all modes are much more than lengths of the corresponding segments, by means of expanding the input expressions into a power series with respect to a small parameter that is the product of wave number by length of the segment, and extracting the leading terms of the series.
[0057] When compiling the formula for merging the segments, it is important to pass from velocities v to average volume flow rate q by means of multiplying the former by cross-sectional areas S:
q=Sv (12)
[0058] The relationships given above remain unchanged, but the scale of the impedance changes:
Z -> Z S ( 13 ) ##EQU00007##
[0059] If at some point several segments are connected, as is shown in FIG. 2, then conservation of continuity of pressure and volume flow rate is implied
p1=p2= . . . =pN
q1=q2+ . . . +pN (14)
with directions of the axes indicated by arrows. Dividing flow rate by pressure, we obtain the joining equation for impedances:
1 Z 1 = 1 Z 2 + + 1 Z N ( 15 ) ##EQU00008##
[0060] A junction point may possess its own dynamics coded in lumped impedance (s), which is added to the joining equation:
1 Z 1 = 1 Z 2 + + 1 Z N + 1 ζ ( s ) ( 16 ) ##EQU00009##
[0061] This, for example, will be the case when segments are jointed via a small deformable chamber contributing to the equation of volume balance by means of expansion and compression with pressure variation. In a rigid chamber, lumped impedance is infinite and the contribution associated with it equals zero. ζ(s) may provide for conformity to complex conditions of juncture, accounting for the influence in the near-wellbore zone, for example, an effect of perforations and other obstacles, for example, a gravel pack.
[0062] The reservoir also can be considered as an element of lumped impedance. In this case, ζ(s)=Zreservoir (0, s), where Zreservoir (0, s) is point-by-point impedance calculated in the wellbore.
[0063] The procedure of solution of the transmission line is as follows. Boundary conditions are assigned at all ends of the scheme except one ("intake of the electric submersible pump") and the corresponding values of impedance are determined. Using the impedance transfer equation, values of impedance are calculated at opposite ends of the segments, then for passing to the next segments, the joining equation for impedance is used, and so on, until impedance at the wellbore ZESP (s) is obtained. Then, with consideration of flow rate at the input to the wellbore Q (s) (which may be physically realized, for example, in the form of an active pump with a certain discharge/suction time schedule), the pressure response P(s) can be obtained simply with the use of:
P(s)=ZESP(s)Q(s) (17)
[0064] Qualitative values in the time domain can be obtained, if needed, by applying the inverse Laplace transform.
[0065] The main qualitative characteristics allowing the construction of a model of the transfer line are propagation constants and characteristics of resistances of wellbore cross-sections γ (s), Zr(s) and the lumped impedance of the reservoir at the bottomhole Zreservoir(0, s). Mathematical models exist for both quantitative characteristics. One of them (in the variables pressure/velocity) that is applicable in the low-frequency (<100 Hz) range:
c 2 γ 2 = s 2 1 - 2 J 1 ( Q ) Q J 0 ( Q ) , Q ≡ i R s μ , ( 18 ) Z c ( s ) = ρ c 1 - 2 Q J 1 ( Q ) J 0 ( Q ) ( 19 ) ##EQU00010##
[0066] for laminar flow of a viscous fluid with kinematic viscosity μ in a rigid pipe of a radius R with phase velocity c--see, for example, "A Trikha, An efficient method of simulating frequency-dependent friction in transient liquid flow, Trans. of ASME, J. Bas. Eng., V97 (1975), p. 97-105". Similar expressions can be derived for a structure comprising any number of concentric cylinders, solid or fluid, or the corresponding expressions can be obtained numerically, for example, by the method described in Karpfinger F., Gurevich B., Bakulin A., Modeling of wave dispersion along cylindrical structures using the spectral method, J. Acoust. Soc. Am., 2008, Aug., 124(2), p. 859-865.
[0067] For a description of the reservoir, it is possible to derive a model of the reservoir response or to utilize an already known model. For example, the following result of the theory of harmonic tests describes an axisymmetric isotropic reservoir with a circular zone of local permeability reduction around a non-cased wellbore
Z reservoir ( 0 , s ) = η R k ( log ( 2 σ - 1 2 ) + 1 - α α log ( λ ) - + O ( slog ( s ) ) ) , σ ≡ R 2 κ s , ( 20 ) ##EQU00011##
[0068] where R is a radius of the well, Y≈1,781 . . . is the Euler's constant, η is a viscosity of the formation fluid, k is a formation permeability, κ=k/φηct, where ct is an overall compressibility coefficient of the rock filled with the formation fluid, φ is porosity of the reservoir formation, α is local reduction of permeability (the ratio of permeability of the local permeability reduction zone to permeability of the reservoir), λ is radius of the zone of local permeability reduction in the units of wellbore radius.
[0069] The example in FIG. 3 illustrates sensitivity of ZESP to parameters of the reservoir with particular parameters of the geometry schematically displayed in the left. Formation height was 15 m with permeability of 1 Darcy, the model of reservoir formation includes the above-described radial composite model. Four curves in FIG. 3 show the relationship of a module of hydraulic impedance at the intake of the electric submersible pump versus frequency, for non-perforated well and for a perforated well with three variants of a zone of local permeability reduction described in the upper left-hand corner of the diagram. It can be seen that sensitivity is especially high around the resonance and antiresonance peaks.
[0070] One of the methods for correlating the model to the experiment is utilization of at least two sensors for measurement of pressure and an analog of flow rate, for example, vertical velocity of the fluid, where "vertical" means the direction of the wellbore axis at the place of measurement, determining the relation of their spectra that is the point-by-point impedance, and correlating it to the value of the model. This is the most complete method, but uses measurement of two quantitative characteristics.
[0071] Another method comprises measuring a quantitative characteristic, for example, pressure, and determining how its spectrum varies with time, for example, by determining consecutive spectral relationships:
N ( s t k ) = P ( s t k + 1 ) P ( s t k ) ( 21 ) ##EQU00012##
[0072] Provided that the input electric signal into the electric submersible pump pertaining to different time periods is the same, one can reasonably assume that rotation speed of the impeller will be the same and for this reason flow rate will also be the same, hence:
P(s|tk)=ZESP(s|tk)Q(s) (22)
and
N ( s t k ) = Z ESP ( s t k + 1 ) Z ESP ( s t k ) ( 23 ) ##EQU00013##
[0073] Thus, we obtain the relationship in which the measured quantitative characteristic N(s|tk) can be correlated to the relative change in impedance at the intake of the pump, which follows from the model. Similar relationships can be written for any point of the bottomhole chamber. Thus, this method is suitable for determining changes in parameters of the bottomhole chamber.
[0074] The origin of the resonance and anti-resonance peaks in the spectra is caused by the generation of standing waves in the segments included in the circuit of the transmission line. Maxima/minima appear in segments and for this reason impedance is considered as a function of the Lalpacian s-variable, possesses poles/zeros, and when the latter are closer to the imaginary axis, they lead to continuity to the corresponding maxima and minima on the imaginary axis. If one carefully examines the impedance transfer equation, it is easy to establish that, as a rule, maxima/minima of the input impedance appear in the area of the frequency multiple of half or quarter the length of the corresponding segments. The conditions of a resonance/anti-resonance is as follows:
c ( v ) 4 v = L n , n = 3 , 5 , 7 2 , 4 , 6 ( 24 ) ##EQU00014##
where c(v) is phase velocity of the tube wave v, and L is length of the segment. With consideration of the weak dependence of c on v, the interval between two resonance frequencies can be approximated as
Δ v = c 2 L ( 25 ) ##EQU00015##
[0075] When several segments are joined, a structure with more complex poles appears. In particular, the main harmonic series for non-perforated wells and wells with a minimal permeability reduction is explained by formation of a standing wave in the 3-segment circuit where the first segment is directly below the electric submersible pump, the second segment is above the reservoir and the third one is below the reservoir; with the interval of approximately 2.2 Hz that corresponds to (25) where c=800 m/s is the phase velocity utilized in the model, and L=160 m is the distance from the electric submersible pump to the bottomhole of the well. Thus, if geometry of the bottomhole chamber is known, by correlating the resonance/anti-resonance frequencies included in the model it is possible to determine phase velocity of the tube waves. Velocity of the tube waves c is a function of conformability of the pipes and the phase velocity of the fluid C in the unlimited medium. The latter velocity value correlates to oscillations of pressure and density in the following way
δp=c2δρ (26)
and, for this reason, it makes it possible to measure a compressibility coefficient of the fluid. Coefficient of compressibility of the fluid, in turn, may strongly vary if gas is present in the fluid. For example, for a simple two-phase mixture (a liquid and an ideal gas):
c 2 = Np ρ ( 1 - Γ ) Γ ( 27 ) ##EQU00016##
where p is background pressure, ρ is density of the fluid without the gas, F is the volume ratio of the gas of the "quality factor" and N is the exponent of polytropic expansion. This formula is applicable with respect to values of F, which are not too close to 0 or 1; in the latter case a more complex formula applies. For multiphase, multicomponent liquid-gas mixtures, dependencies of sound velocity versus volume ratios of phases can be either measured in the laboratory or obtained theoretically. The described method makes it possible to measure volume ratio of gas in the zone below the pump and, on a more general case, to obtain data for determining properties of a multicomponent fluid, which depend on compressibility coefficient, by means of correlating the structure of resonance and antiresonance peaks in any of the quantitative characteristics measured in the wellbore, in particular,--in pressure or hydraulic impedance measured in a point or in a multitude of points in the bottomhole chamber.
[0076] Although only a few examples have been described in detail above, those skilled in the art will readily appreciate that many modifications are possible in the examples without materially departing from this subject disclosure. Accordingly, all such modifications are intended to be included within the scope of this disclosure as defined in the following claims. In the claims, means-plus-function clauses are intended to cover the structures described herein as performing the recited function and not only structural equivalents, but also equivalent structures. Thus, although a nail and a screw may not be structural equivalents in that a nail employs a cylindrical surface to secure wooden parts together, whereas a screw employs a helical surface, in the environment of fastening wooden parts, a nail and a screw may be equivalent structures. It is the express intention of the applicant not to invoke 35 U.S.C. §112, paragraph 6 for any limitations of any of the claims herein, except for those in which the claim expressly uses the words `means for` together with an associated function.
User Contributions:
Comment about this patent or add new information about this topic: