Patent application title: COMPACT INDUCTOR EMPLOYING REDISTRUBUTED MAGNETIC FLUX
Inventors:
Khai Doan The Ngo (Blacksburg, VA, US)
Han Cui (Blacksburg, VA, US)
IPC8 Class: AH01F2728FI
USPC Class:
Class name:
Publication date: 2015-10-01
Patent application number: 20150279548
Abstract:
The present invention is directed to a compact inductor having the
required (predetermined) inductance and current rating, further designed
to avoid substantial heat generation by avoiding saturation, winding(s)
possessing a low DC resistance and copper loss, and minimizing the
required volume or profile in order to conserve circuit board
real-estate. The compact inductor design of the present invention
includes both enclosed core as well as enclosed winding type of inductor
designs.Claims:
1. A compact balanced field enclosed winding inductor comprising: a first
core; a first winding having a first end and a second end, said first
winding adapted to spiral inwardly from said first end and terminates at
said second end at a point substantially central to said first winding to
form a first spiral of a first shape in a first plane, wherein said first
winding is embedded in said first core; a second core; and a second
winding having a first end and a second end, said second winding adapted
to spiral inwardly from said first end of said second winding and
terminates at said second end of said second winding at a point
substantially central to said second winding to form a second spiral of a
second shape in a second plane, wherein said second winding is embedded
in said second core and said second end of said second winding is
electrically connected to said second end of said first winding.
2. The compact balanced field enclosed winding inductor of claim 1, wherein said core comprises a magnetically permeable material.
3. The compact balanced field enclosed winding inductor of claim 1, wherein said winding comprises a winding wire.
4. The compact balanced field enclosed winding inductor of claim 1, wherein at least one of said first shape and second shape is selected from the group consisting of circular and rectangular.
5. A compact balanced field enclosed core inductor comprising: a plurality of interdependent cores having similar shape in order to enable nesting, wherein an interdependent second core is nested within an interdependent first core having a slot-width between said interdependent first core and said interdependent second core to permit the passing of an interdependent winding.
6. The compact balanced field enclosed core inductor of claim 5, further comprising at least one interdependent cored nested within said interdependent second core.
7. The compact balanced field enclosed core inductor of claim 5, wherein said winding comprises a winding wire.
8. The compact balanced field enclosed core inductor of claim 5, wherein at least one of said interdependent first core and said interdependent second core comprises a magnetically permeable material.
9. The compact balanced field enclosed core inductor of claim 5, wherein at least one of said interdependent first core and said interdependent second core comprises a cross-sectional shape defined by a shape selected from the group consisting of a rectangle and circle.
10. The compact balanced field enclosed core inductor of claim 5, wherein said interdependent winding comprises a cross-sectional shape is a defined by a shape selected from the group consisting of a rectangle and circle.
11. A method of constructing a compact balanced field enclosed winding inductor having a desired inductance Lo and a desired resistance Ro, at least a first winding window and a second winding window, said method comprising: (a) predetermining a uniformity factor α of the compact balanced field enclosed winding inductor to a minimal value sufficient to maintain the benefit of a balanced field; (b) determining a plate thickness Hp, outer radius of the first winding window RO1, inner radius of the first winding window RI1, and outer radius of the second winding window RO2 of the compact balanced field enclosed winding inductor simultaneously; (c) determining the radii of the remaining winding windows of the at least two winding windows of the compact balanced field enclosed winding inductor recursively, wherein the radii determined are limited by manufacturing constraints; (d) determining the number of turns nj of each of the at least two winding windows of the compact balanced field enclosed winding inductor; and (e) determining the inductance L and resistance Rdc of the compact balanced field enclosed winding inductor, wherein if the inductance L is not greater or equal to the desired inductance Lo and the resistance is not less than or equal to a desired resistance Ro, the uniformity factor α is increased and steps (b)-(e) are repeated.
12. A method of constructing a compact balanced field enclosed core inductor having a desired inductance Lo and a desired resistance Ro and at least two interdependent cores, wherein a second interdependent core is nested within a first interdependent core, said method comprising: (a) predetermining the uniformity factor α of the compact balanced field enclosed core inductor to a minimal value sufficient to maintain the benefit of a balanced field; (b) determining the outer radius RO and the inner radius RI of each of said at least two interdependent cores; (c) determining the ampere-turns NI between the outer radius RO of an outer core and the outer radius RO of a core nested within the outer core of said at least two interdependent cores; and (d) determining the stored energy E, inductance L and resistance Rdc of the enclosed core inductor, wherein if the inductance L is not equal to a desired inductance Lo and the resistance Rdc is not equal to a desired resistance Ro, the uniformity factor α is increased and steps (b)-(d) are repeated.
Description:
PRIORITY CLAIM AND RELATED APPLICATIONS
[0001] This non-provisional application claims the benefit of priority from provisional application U.S. Ser. No. 61/973,594 filed on Apr. 1, 2014 and provisional application U.S. Ser. No. 62/140,074 filed on Mar. 30, 2015. Each of said applications is incorporated by reference in its entirety.
BACKGROUND OF THE INVENTION
[0002] 1. The Field of the Invention
[0003] This invention generally relates to inductor devices. In a more specific aspect, the present invention is directed to an inductor having a compact design enabled by the redistribution of magnetic flux.
[0004] 2. Background Art
[0005] Power transformers and power inductors are important components of every switching converters or circuits. During the turn-on switching period, the passive components store the energy in the form of magnetic flux, and during the turn-off switching period they transfer the stored energy to the load side. Often the high-frequency Alternating Current (AC) ripple superimposed on the inductor current prevents a substantial portion of the power from being transferred to the load. The core loss includes hysteresis loss and eddy current loss, and higher operation frequency usually results in higher core loss. This power loss is dissipated in the core in the form of heat and sometimes noise (mechanical vibrations). The core loss consists of hysteresis loss and eddy current loss. Typically the higher operation frequency, the higher core losses. Another source of inductor power loss is directed to the inductor's winding(s), commonly called the winding loss. This power loss is primarily due to the resistance of the conductor material (e.g. wire), that comprises the winding; this power loss is dissipated in the winding in the form of heat. A common solution to dealing with inductor heat issues, which include hot spots, include introducing heat sinks, designs that promote air cooling, larger diameter winding wire (to reduce ohmic based power loss), and the like. Further, saturation shall be reduced. Unfortunately, all of the aforementioned solutions result in the creation of an inductor having larger volume which is direct opposition to modern day technology forces, which are driving electrical-electronic circuit toward more compact, efficient, and cost effective type designs. There exists a long felt need to reduce the package size of inductor type devices because these magnetic based components are notorious for consuming large amounts of real-estate on circuit boards.
[0006] Known in the electrical or electronic arts are inductive devices, which are passive electrical type devices. Inductive devices also known by other names, including chokes, toroids, coils, or simply inductors. These devices are commonly used on electronic circuits to provide inductance, which is an electrical property that serves as a means for storing electrical energy in a magnetic field. Such devices are typically used in conjunction with time varying or alternating current applications. In general, there are two common types of Inductor designs, the enclosed core and the enclosed winding. The enclosed core type inductor is typically configured using one or more coils or windings which is typically wrapped around a magnetically permeable core. So-called "dual winding" inductors utilize two windings wrapped around a common core. The enclosed winding type of inductor is typically structured having a magnetically permeable type material enveloping the winding(s) portion of the device.
[0007] Accordingly, in view of the foregoing present day inductor deficiencies, there exists a clear motivation in the electrical arts for new and useful inductor improvements.
SUMMARY OF THE INVENTION
[0008] Passive components, e.g., inductors and capacitors are bulky parts on circuit boards. Researchers in academia, government, and industry have been searching for ways to improve the magnetic energy density and reduce the package size of magnetic parts. The present invention is directed to a compact inductor configured to avoid substantial heat generation by avoiding saturation, reducing the Direct Current (DC) resistance of the winding(s) and copper loss, reducing the required physical volume or profile to conserve circuit board real-estate and increase the inductance of the compact inductor. Thus, there is a demand for uniform distribution of magnetic field and energy in the core without crowding the flux in an inductor.
[0009] In accordance with the present invention, there is provided a compact balanced field enclosed winding inductor including:
[0010] a first core;
[0011] a first winding having a first end and a second end, the first winding adapted to spiral inwardly from the first end and terminates at the second end at a point substantially central to the first winding to form a first spiral of a first shape in a first plane, wherein the first winding is embedded in the first core;
[0012] a second core; and
[0013] a second winding having a first end and a second end, the second winding adapted to spiral inwardly from the first end of the second winding and terminates at the second end of the second winding at a point substantially central to the second winding to form a second spiral of a second shape in a second plane, wherein the second winding is embedded in the second core and the second end of the second winding is electrically connected to the second end of the first winding. In one embodiment, the first core includes a magnetically permeable material. In one embodiment, the first winding includes a winding wire. In one embodiment, the first shape is circular. In another embodiment, the first shape is rectangular.
[0014] There is further provided a compact balanced field enclosed core inductor including: a plurality of interdependent cores having similar shape in order to enable nesting, wherein an interdependent second core is nested within an interdependent first core having a slot-width between the interdependent first core and the interdependent second core to permit the passing of an interdependent winding.
[0015] In one embodiment, the compact balanced field enclosed core inductor further includes at least one interdependent cored nested within the interdependent second core. In one embodiment, the interdependent winding includes a winding wire.
[0016] In one embodiment, the at least one of the interdependent first core and the interdependent second core includes a magnetically permeable material.
[0017] In one embodiment, at least one of the interdependent first core and the interdependent second core includes a cross-sectional shape defined by the shape of a rectangle. In another embodiment, the at least one of the interdependent first core and the interdependent second core includes a cross-sectional shape defined by the shape of a circle.
[0018] In one embodiment, the interdependent winding includes a cross-sectional shape defined by a rectangle. In another embodiment, the interdependent winding includes a cross-sectional shape defined by a circle.
[0019] There is further provided a method of constructing a compact balanced field enclosed winding inductor having a desired inductance Lo, a desired resistance Ro, at least a first winding window and a second winding window, the method including:
[0020] (a) predetermining the uniformity factor α of the balanced field enclosed winding inductor to a minimal value sufficient to maintain the benefit of a balanced field;
[0021] (b) determining the plate thickness Hp, outer radius of the first winding window RO1, inner radius of the first winding window RI1, and outer radius of the second winding window RO2 simultaneously;
[0022] (c) determining the radii of the remaining winding windows of the at least two winding windows recursively, wherein the radii determined are limited by manufacturing constraints;
[0023] (d) determining the number of turns nj of each of the at least two winding windows; and
[0024] (e) determining the inductance L and resistance Rdc of the enclosed winding inductor, wherein if the inductance Rdc is not greater or equal to a desired inductance Lo and the resistance is not less than or equal to a desired resistance Ro, the uniformity factor α is increased and steps (b)-(e) are repeated.
[0025] There is further provided a method of constructing a compact balanced field enclosed core inductor having a desired inductance Lo, a desired resistance Ro and at least two interdependent cores, wherein a second interdependent core is nested within a first interdependent core, the method including:
[0026] (a) predetermining the uniformity factor α of the balanced field enclosed core inductor to a minimal value sufficient to maintain the benefit of a balanced field;
[0027] (b) determining the outer radius RO and the inner radius RI of each of the at least two interdependent cores;
[0028] (c) determining the ampere-turns NI between the outer radius RO of an outer core and the outer radius RO of a core nested within the outer core of the at least two interdependent cores; and
[0029] (d) determining the stored energy E, inductance L and resistance Rdc of the enclosed core inductor, wherein if the inductance L is not equal to a desired inductance Lo and the resistance Rdc is not equal to a desired resistance Ro, the uniformity factor α is increased and steps (b)-(d) are repeated.
[0030] Accordingly, it is an object of the present invention to provide an inductor capable of meeting operational requirements of the inductor by coming in a smaller package, thereby requiring less space on the circuit board to which the inductor is used.
[0031] It is another object of the present invention to provide a method for constructing a compact balanced field enclosed core or enclosed winding inductor.
[0032] It is another object of the present invention to provide, in one embodiment, an inductor where previously unused space is populated with magnetic flux-increasing components, thereby maintaining the physical size of the inductor as those of conventional inductors but with increased energy storage.
[0033] It is another object of the present invention to provide an inductor having a suitably low resistance that reduces heat issues.
[0034] It is another object of the present invention to provide an inductor having no magnetic flux saturation issues, thereby capable of higher energy storage compared to an inductor with such issues within the same inductor size constraints.
[0035] It is another object of this invention to provide a relatively simple system that is economical from the viewpoint of the manufacturer and consumer, is susceptible to low manufacturing costs with regard to labor and materials, and which accordingly evokes low prices for the consuming public, thereby making it economically available to the buying public.
[0036] Whereas there may be many embodiments of the present invention, each embodiment may meet one or more of the foregoing recited objects in any combination. It is not intended that each embodiment will necessarily meet each objective.
[0037] Thus, having broadly outlined the more important features of the present invention in order that the detailed description thereof may be better understood, and that the present contribution to the art may be better appreciated, there are, of course, additional features of the present invention that will be described herein and will form a part of the subject matter of this specification.
[0038] In this respect, before explaining at least one embodiment of the invention in detail, it is to be understood that the invention is not limited in its application to the details of construction and the arrangements of the components set forth in the following description or illustrated in the drawings. The present invention is capable of other embodiments and of being practiced and carried out in various ways. Also it is to be understood that the phraseology and terminology employed herein are for the purpose of description and should not be regarded as limiting.
[0039] As such, those skilled in the art will appreciate that the conception, upon which this disclosure is based, may readily be utilized as a basis for the designing of other structures, methods and systems for carrying out the several purposes of the present invention. It is important, therefore, that the claims be regarded as including such equivalent construction insofar as they do not depart from the spirit and scope of the conception regarded as the present invention.
BRIEF DESCRIPTION OF THE DRAWINGS
[0040] In order that the manner in which the above-recited and other advantages and objects of the invention are obtained, a more particular description of the invention briefly described above will be rendered by reference to specific embodiments thereof which are illustrated in the appended drawings. Understanding that these drawings depict only typical embodiments of the invention and are not therefore to be considered to be limiting of its scope, the invention will be described and explained with additional specificity and detail through the use of the accompanying drawings in which:
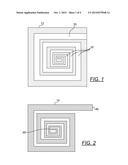
[0041] FIG. 1 is a top view of an enclosed-winding inductor according to one embodiment of the present inductor, depicting a core without windings.
[0042] FIG. 2 is a top view of a winding according to one embodiment of the present inductor, depicting the winding configured to be disposed within the core of FIG. 1.
[0043] FIG. 3 is a top view showing a winding having been disposed in the winding windows of a core.
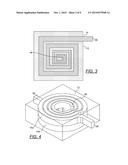
[0044] FIG. 4 is a top perspective view of two windings disposed in a core.
[0045] FIG. 5 is a side view of two windings disposed in a core.
[0046] FIG. 5A is a top view of one winding disposed in a core.
[0047] FIG. 6 is an axisymmetric view of an enclosed-winding inductor showing three winding windows, ampere-turn direction, and magnetic flux path.
[0048] FIG. 7 is an axisymmetric view of a balanced field inductor showing the flux drop on the vertical direction by a factor of a, ampere loops around winding window 1, and magnetic flux path.
[0049] FIG. 8 is a flowchart depicting the steps by which the enclosed winding type of the present inductor is configured.
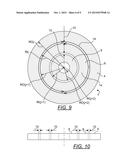
[0050] FIG. 9 is a top view of an inductor according to one embodiment of the present inductor, depicting an inductor without windings.
[0051] FIG. 10 is a side partially transparent view of an inductor according to one embodiment of the present inductor, depicting the inductor without windings.
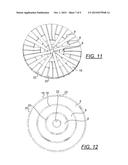
[0052] FIG. 11 is a top view of an inductor according to one embodiment of the present inductor, depicting the inductor with windings.
[0053] FIG. 12 is a top view of an inductor according to one embodiment of the present inductor, depicting the windings through various cores.
[0054] FIG. 13 is a flowchart depicting the steps by which the enclosed core type of the present inductor is configured.
[0055] FIG. 14 depicts an equivalent circuit of an inductor.
[0056] FIG. 15 depicts an example of modified structure of winding window j after considering the fabrication clearance on the horizontal and vertical direction where m=3=the number of clearance spacing on the horizontal direction, n=5=the number of clearance spacing on the vertical direction.
PARTS LIST
[0057] 2--inductor
[0058] 4--first core
[0059] 6--second core
[0060] 8--third core
[0061] 10--slotwidth
[0062] 12--core
[0063] 14, 14a, 14b--winding
[0064] 16--bridge
[0065] 18--winding over first core
[0066] 20--winding over second core
[0067] 22--winding over third core
[0068] 24--core height Hc
[0069] 26--window height
[0070] 28--outer radius of core Rc
[0071] 30--winding window
[0072] 32--Gaussian surface
[0073] 34--magnetic flux
[0074] 36--step of predetermining uniformity factor
[0075] 38--step of determining the required geometrical parameters RO and RI of a core
[0076] 40--step of determining Ampere-turns on core
[0077] 42--step of determining the stored energy, inductance and resistance of core
[0078] 44--step of determining whether the calculated stored energy, inductance and resistance of core meet desired values
[0079] 46--first end of winding
[0080] 48--second end of winding
[0081] 50--ampere loop 1
[0082] 52--ampere loop 2
[0083] 54--step of determining Hp, RO1, RI1 and RO2 from Equations E2, E4 and E5
[0084] 56--step of determining all other radii from Equations E4 and E5, within limits of Nw by manufacturing constraints
[0085] 58--step of determining the number of turns nj from Equations E7 and E8
[0086] 60--step of determining inductance L and resistance Rdc from Equations E13 and E15 and comparing inductance L with desired inductance Lo and resistance Rdc with desired resistance Ro
Particular Advantages of the Invention
[0087] The present invention provides a relatively simple, cost-effective, efficient solution directed to present day inductor drawbacks such as size and hot spots. The balanced field compact inductor of the present invention will provide the required (predetermined) inductance and current rating. The uniform magnetic field distribution substantially remedies the long felt issues directed to inductor heat generation, core saturation and non-uniform energy density. Enabled are shorter length windings and smaller cross-sectional areas and physical volumes taken up the present inductors and geometries yielding lower DC resistances and copper losses. Additionally, the present invention minimizes the required volume or profile in order to conserve circuit board real-estate. The compact inductor design of the present invention includes both enclosed core as well as enclosed winding type of inductor designs.
DEFINITIONS OF TERMS USED IN THIS SPECIFICATION
[0088] The balanced field inductor type devices (i.e., enclosed core, enclosed winding) discussed throughout this disclosure shall have equivalent nomenclature, including the device, the inductor, the system, the present invention, or the invention. Additionally, the term exemplary shall possess a single meaning throughout this disclosure; wherein the sole definition pertains to serving as an example, instance, or illustration.
[0089] The term core or magnetic core is defined as a magnetically permeable member having circular, ring like geometry or rectangular, ring like geometry with circular or rectangular cross-sectional shape.
[0090] The term winding wire is defined as a conductor comprising the inductor winding, the winding wire can be configured from a variety of wire geometries (i.e., cross-sectional area and cross-sectional area shape). Cross-sectional area shapes include the typical circular configuration, as well as rectangular geometries that possess a relatively lower resistance due to a relatively larger cross-sectional area.
[0091] The term "balanced field" or "redistributed flux" shall be used herein to reference uniform magnetic flux, i.e., the amount of magnetic field passing through a surface is uniformly distributed. When the term "balanced field" is used in conjunction with the term "inductor," it modifies the meaning of the term "inductor" to indicate an inductor or components of an inductor with a high uniformity factor α or a low saturation condition.
[0092] The term α is defined as the uniformity factor of an inductor.
[0093] The term ATj is defined as the Ampere-turns in winding window j.
[0094] The term Bmax is defined as the maximum flux density achievable in a core.
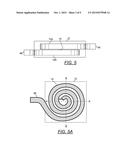
[0095] The term Bs is the saturation flux density of a core.
[0096] The term E is defined as the energy stored in a core of an inductor.
[0097] The term B is defined as the flux density of a core.
[0098] The term H is defined as the magnetic field of an inductor.
[0099] The term N is defined as the total number of winding turns.
[0100] The term Hc is defined as the height of a core.
[0101] The term Hp is defined as the plate thickness between winding and core.
[0102] The term Hw is defined as the winding thickness.
[0103] The term Ir is defined as the current rating of a winding.
[0104] The term L is defined as the inductance of an inductor.
[0105] The term μ is defined as the permeability of a core material.
[0106] The term μo is defined as the vacuum permeability.
[0107] The term nj is defined as the number of turns in winding window j.
[0108] The term Nw is defined as the number of winding windows.
[0109] The term ρcu is defined as the copper resistivity.
[0110] The term Rc is defined as the outer radius of a core.
[0111] The term Rdc is defined as the DC resistance of an inductor.
[0112] The term ROj is defined as the outer radius of winding window j.
[0113] The term RIj is defined as the inner radius of winding window j.
[0114] The term Pohm--.sub.loss is defined as the DC winding loss.
[0115] The term V is defined as the effective volume of energy storage.
[0116] The term T is defined as the time constant (L/Rdc) of an inductor.
[0117] The term TV is defined as the time-constant-density (L/RdcV) of an inductor.
[0118] The term Lo is defined as the desired inductance.
[0119] The term Ro is defined as the desired resistance.
DETAILED DESCRIPTION OF A PREFERRED EMBODIMENT
[0120] The term "about" is used herein to mean approximately, roughly, around, or in the region of. When the term "about" is used in conjunction with a numerical range, it modifies that range by extending the boundaries above and below the numerical values set forth. In general, the term "about" is used herein to modify a numerical value above and below the stated value by a variance of 20 percent up or down (higher or lower).
[0121] With reference to the drawings of the present invention, several embodiments pertaining to the compact inductor of the present invention thereof will be described. In describing the embodiments illustrated in the drawings, specific terminology will be used for the sake of clarity. However, the invention is not intended to be limited to the specific terms so selected, and it is to be understood that each specific term includes all technical equivalents that operate in a similar manner to accomplish a similar purpose. Terminology of similar import other than the words specifically mentioned above likewise is to be considered as being used for purposes of convenience rather than in any limiting sense.
[0122] It must be noted that as used herein and in the appended claims, the singular forms "a", "an", and "the" include plural reference unless the context clearly dictates otherwise. As well, the terms "a" (or "an"), "one or more" and "at least one" can be used interchangeably herein. It is also to be noted that the terms "comprising", "including", "characterized by", "possessing" and "having" are all to be interpreted as open ended terms, are all considered equivalent terms, and are used interchangeably.
[0123] Disclosed herein are two basic types of inductors, i.e., enclosed winding and enclosed core inductors and corresponding embodiment. The primary goal for each embodiment of the present inductor is to achieve high magnetic-energy density by distributing the magnetic flux uniformly, leading to inductor geometries with a volume significantly lower than that of conventional inductors. A relatively uniform flux distribution is advantageous not only from the density standpoint, but also from the thermal standpoint via the reduction of hot spots, and from the reliability standpoint via the suppression of flux crowding. For toroidal inductors of the enclosed core type, adding concentric toroidal cells of magnetic material and distributing the windings properly can successfully make the flux density distribution uniform and thus significantly improve the power density. Compared with a conventional toroidal inductor, the balanced field inductor introduced herein has an enclosed-winding geometry. The winding layout inside the core is configured to distribute the magnetic flux relatively uniformly throughout the magnetic volume to obtain a higher energy density and smaller package volume than those of a conventional toroidal inductor.
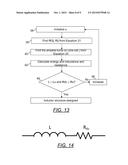
[0124] The uniformity factor α is defined to reflect the uniformity level inside a core volume. For each given magnetic material and given volume, an optimal uniformity factor exists, which has the highest time constant. The time constant varies with the footprint area, inductor thickness, relative permeability of the magnetic material, and uniformity factor. Therefore, the objective for the balanced field inductor design is to seek the highest possible time constant, so that the balanced field inductor gives a higher inductance and/or lower resistance than conventional inductors of the same volume. In one embodiment, the calculated time-constant-density of the balanced field inductor designed is 4,008 s/m3, which is more than two times larger than the 1,463 s/m3 of a conventional inductor.
[0125] Enclosed Winding Inductor
[0126] A balanced field enclosed winding inductor includes a distributed winding structure enclosed by a core. The winding structure is configured to distribute magnetic flux in a shaped pattern. The core is made of a magnetic material, e.g., iron powder, and it delineates the footprint area and the total thickness of the inductor. The winding structure typically follows a spiral pattern surrounded by magnetic flux generated by current excitation. The enclosed-winding geometry has the winding structure configured to distribute the magnetic flux into a uniform shape. For a given set of input parameters such as the footprint, thickness of the inductor, permeability of the magnetic material, and highest flux density allowed from the core loss limitation, the radii of each winding window can be determined sequentially according to the uniformity factor selected. After the winding structure is determined, the total energy stored in the core volume and the total DC winding loss can be calculated, and yield the inductance and resistance of the inductor. In one embodiment, a balanced field inductor of a volume of 10×10×2 mm3 for L=1.6 μH, Ir=10 A, and Rdc=7.0 mΩ is contrasted to a conventional inductor with comparable electronic ratings (L=1.5 μH, Ir=10 A, and Rdc=8.1 mΩ) but occupies 10.3×10.5×4 mm3, i.e., more than two times the volume of the balanced field inductor. The time constant, which is defined as the ratio of inductance to resistance, is an important factor to evaluate the performance of an inductor. A higher time constant suggests higher energy, but with minimum loss within a given volume. The objective of the balanced field inductor is to optimize all the parameters so that the highest time constant can be achieved. Several parameters such as the uniformity factor, the footprint and thickness, the permeability, and the maximum flux density are studied to obtain their relationships with the time constant. For a given volume, an optimized uniformity factor α exists, which has the peak value of the time constant, while different footprints and thicknesses yield different optimal values of α. The time constant increases with increasing volume, since a larger volume provides more space for energy storage. The magnetic properties of the core material is another factor that affects the time constant. At a given volume, the time constant increases proportionally with the permeability, while the maximum flux density has no influence on the time constant at all. Comparisons of the balanced field inductors with the conventional inductors show that the time constant of the balanced field inductors is about 2.5 times higher than that of the conventional inductors at the same volume, or that the volume of the balanced field inductor is two times smaller than that of the commercial product at the same value of time constant because of the better utilization of the magnetic material.
[0127] FIG. 1 is a top view of an enclosed winding inductor 2 according to one embodiment of the present inductor, depicting a core 12 without a winding 14. A core 12 can be manufactured from a suitable core material provided, in this example, in a rectangular shaped plate, by laser ablation where the non-shaded portions are removed to a suitable depth to result in winding windows 30 to accommodate a winding. FIG. 2 is a top view of a winding 14 according to one embodiment of the present inductor, depicting the winding 14 configured to be disposed within the core 12 shown in FIG. 1. FIG. 3 is a top view showing a winding 14 having been disposed in the winding windows 30 of a core 12.
[0128] FIG. 4 is a top perspective view of two windings 14a and 14b disposed in a core 12. FIGS. 1-3 depict a winding 14 formed in a rectangular manner. FIG. 5 is a side view of two windings 14 disposed in a core 12. FIG. 4 depicts two windings 14, each having a terminal at a first end 46 and a second end 48 at which a second winding 14 can be electrically connected via a bridge 16. It shall be noted that the winding 14 disposed on the top winding 14 is configured to spiral in clockwise direction (as viewed from the top) toward the center, connects to the second end of the bottom winding 14, also at its second end 48 via bridge 16. The second winding 14 continues to spiral in clockwise direction (as viewed from the top) to a bottom terminal at the first end 46 of the bottom winding 14. In one embodiment, the vertical spacing between adjacent windings is kept at no less than about 0.2 mm. The core may be a composite of two halves connected in their medial position. The core may also be a core similar to that shown in FIG. 1, but instead configured in the shape and size of the corresponding windings and configured to accommodate not one but two windings. It shall also be noted that the windings 14a, 14b, of FIG. 4 may be configured in a circular manner having a winding cross-sectional shape of a rectangle.
[0129] FIG. 5A is a top view of one winding disposed in a core. FIG. 6 is an axisymmetric view of an enclosed winding inductor showing three winding windows 30, ampere-turn direction, and magnetic flux 34 path as a result of viewing the upper right section of the core 12 as taken along lines AA and BB of FIG. 5A with a line of sight perpendicular to line AA. Referring to FIG. 6, an enclosed-winding inductor 2 includes a magnetic core 12 with a plurality of winding windows 30, each denoted by the letter j. For convenience, the winding windows 30 are numbered from the outer edge of the core to the center of the core. Each winding window carries a prescribed number of ampere-turns ATj in winding window j to ensure uniformity of the flux distribution throughout the core volume.
[0130] The outer and inner radius of each winding window j is denoted by ROj and RIj respectively. For a given footprint diameter or 2*Rc and total inductor/core height of 24 or Hc, the objective of the balanced field design is to optimize the radii of the winding windows, as well as the ampere-turns in each winding window 30, to distribute the magnetic flux as uniformly as possible.
[0131] For a given core loss density and frequency of operation, the maximum magnetic flux density Bmax can be determined from the magnetic properties of the material. The magnetic field around winding window j is allowed to drop from a maximum value Bmax to a minimum value αBmax, where α=uniformity factor and α<1. "Balanced field" flux is achieved when the uniformity factor α approaches unity, implying uniform flux density everywhere throughout the core volume.
[0132] FIG. 6 depicts an inductor with three winding windows. In one embodiment, an inductor having two halves, each having the specifications as follows was tested:
[0133] Winding window j=1, ROj=4.8 mm, RIj=3.8 mm,
[0134] Winding window j=2, ROj=3.6 mm, RIj=2.9 mm,
[0135] Winding window j=3, ROj=2.7 mm, RIj=1.9 mm,
[0136] Winding window j=4, ROj=1.5 mm, RIj=1.0 mm,
[0137] Thickness of winding=0.5 mm,
[0138] Height of an inductor half Hc=1.0 mm
[0139] Footprint of an inductor half=10 mm×10 mm
[0140] Winding cross-sectional shape=square
[0141] Inductance=1.53 μH
[0142] Winding resistance=7.3 mΩ
[0143] In order to find the saturation current of the inductor designed, a current of 8 A-38 A is applied to the inductor. With an assumed 0.9 T saturation flux density, the inductance dropped by 20% when the applied current is about 32 A. Therefore, the saturation current is found to be about 32 A. Compared to a comparable conventional inductor, the present inductor yields a saturation current that is improved by 18% due to the uniformity of the flux distribution.
[0144] An inductor can be considered as a RL circuit, which has an ideal inductor in series with a wire resistor, as shown in FIG. 14. The time constant T of a series RL circuit is defined as the inductance divided by the resistance as shown in equation E1 where L=inductance of inductor and Rdc=DC resistance of inductor.
τ = L R dc Equation E1 ##EQU00001##
[0145] In the balanced field inductor design, the time constant is employed to represent the ratio of the inductance to DC resistance. It shall be noted that at a given inductance, the DC winding resistance decreases with an increasing time constant, thereby decreasing the DC loss due to Rdc.
[0146] The flux density is at its maximum value Bmax at the inner radius of each winding window, and drops by a factor of a along both the radial and vertical directions. Along the vertical edges of the winding windows, the flux density is assumed to be constant. Based on Gauss' law, the amount of flux that flows into a surface equals to the amount of flux that flows out of the surface. Therefore, the behavioral model of the balanced field inductor can be derived based on the Gaussian surfaces defined at different locations. In the case of winding window j=1, the equation for Gaussian Surface Sc can be written as equation E2.
2 π R o 1 H p ( α + α 2 ) B max 2 = π ( R c 2 - R o 1 2 ) ( α + α 2 ) B max 2 or R o 1 2 + 2 R o 1 H p - R c 2 = 0 Equation E2 ##EQU00002##
where Hp is the plate thickness 24, α=uniformity factor, Bmax=maximum flux density, Rc=outer radius of core 28, RO=outer radius of winding window and RI=inner radius of winding window.
[0147] Based on the simplified equation E2 and given Hp and Rc due to physical constraints or desired size limitations governing the core to be made, the outer radius RO of winding window j=1 is thus determined. The plate thickness between winding and core Hp is related to the winding thickness Hw by equation E3.
H p = 1 2 ( H c - H w ) Equation E3 ##EQU00003##
[0148] For the Gaussian surfaces, e.g., Sa, the flux flows from the inner radius to the outer radius of winding window j. For each winding window, the ratio of outer radius to the inner radius is related to the magnetic flux density as shown in equation E4.
R Oj R Ij = B max α B max = 1 α , 1 ≦ j ≦ N w Equation E4 ##EQU00004##
[0149] Where Nw=number of winding windows, Bmax=maximum flux density, j=winding window, ROj=outer radius of winding window j, RIj=inner radius of winding window j and α=uniformity factor.
[0150] Thus, RI1 can be determined once RO1 is known, and RIj can be obtained recursively from ROj. Based on the Gaussian surface Sb defined in FIG. 6, equation E5 yields recursively the outer radius of winding window j>1:
α + α 2 2 B max 2 π R O ( j + 1 ) H p + 1 + α 2 B max π ( R Ij 2 - R O ( j + 1 ) 2 ) = 1 + α 2 B max 2 π R Ij H p or R O ( j + 1 ) 2 - 2 α R O ( j + 1 ) H p + 2 R Ij H p - R Ij 2 = 0 , 1 ≦ j ≦ N w Equation E5 ##EQU00005##
where α=uniformity factor, Hp=plate thickness between winding and core, Bmax=maximum flux density, j=first core, (j+1)=second core, RO(j+1)=outer radius of winding window (j+1), RI(j+1)=inner radius of winding window (j+1) and Rc=outer radius of first core.
[0151] When Hp is not known, e.g., when the plate thickness to be used is to be determined, Hp can be calculated based on the Ampere's law. As shown in FIG. 6, from the winding to the edge of the core, the flux density is regulated to drop by a factor of α vertically. Therefore, based on Ampere's law, the ampere-loop that covers the same winding window should have equal ampere-turns, and equation E6 can be added to solve the plate thickness between the winding and the core:
∫ l 1 H l 1 = ∫ l 2 α H l 2 H w ( 1 + α ) + 2 R Ij ln ( R Oj R Ij ) = α ( H w + 2 H p ) ( 1 + α ) + 2 α R O 2 ln ( R c R O 2 ) Equation E6 ##EQU00006##
where H=magnetic field, α=uniformity factor, Hw=winding thickness, Hp=plate thickness between winding and core, j=winding window, ROj=outer radius of winding window j, RIj=inner radius of winding window j, Rc=outer radius of core.
[0152] By simultaneously solving equation E6 with equations E2 to E5, the plate thickness Hp and the radii of all the winding windows can be derived recursively. Note that once Hp is determined from the outermost winding window, the value can be assumed to remain constant for other winding windows for simplification. Ideally, each winding window j has a calculated Hp from equation E6, and the larger the j, the larger the Hp.
[0153] FIG. 7 is an axisymmetric view of a balanced field inductor showing the flux drop on the vertical direction by a factor of α, ampere loops around winding window 1, and magnetic flux path.
[0154] In order to calculate the Ampere-turns that should be applied to winding window j, the Ampere-loop 1 (part 50) in FIG. 7 is drawn on every winding window. Based on Ampere's law, Ampere-turn ATj is assigned to winding window j as shown in equation E7.
AT j = H w ( B max μ ± α B max μ ) + 2 B max μ R Ij ln ( R Oj R Ij ) Equation E7 ##EQU00007##
[0155] Where j=winding window, ATj=Ampere-turns in winding window j, Hw=winding thickness, Bmax=maximum flux density, μ=permeability of core material, ROj=outer radius of winding window j, RIj=inner radius of winding window j.
[0156] The number of turns in winding window j is determined using ATj and the rated current Ir as shown in equation E8.
n j = AT j I r Equation E8 ##EQU00008##
[0157] Where j=winding window, nj=number of turns in winding window j, ATj=Ampere-turns in winding window j and Ir=current rating.
[0158] Therefore, the total number of turns is the sum of the number of turns in each winding window as shown in Equation E9.
N = j = 1 N w n j = j = 1 N w AT j I r Equation E9 ##EQU00009##
[0159] Where N=total number of winding turns, j=winding window, Nw=number of winding windows, nj=number of turns in winding window j, ATj=Ampere turns in winding window j and Ir=current rating.
[0160] After all the radii and plate thickness are derived, the structure of the inductor is determined. The energy stored in the inductor can be calculated by integrating the flux density throughout the total core volume as shown in equation E10.
E ≈ 1 2 μ ( B max + α B max 2 ) 2 π ( R c 2 H c - H w 1 N w R Oj 2 - R Ij 2 ) Equation E10 ##EQU00010##
where Hc=core height, Hw=winding thickness, μ=permeability of core material, Bmax=maximum flux density, α=uniformity factor, j=winding window, ROj=outer radius of winding window j, RIj=inner radius of winding window j, Rc=outer radius of core and Nw=number of winding windows.
[0161] The small-signal inductance can be derived as follows:
I r 2 = 1 N 2 ( j = 1 N w AT j ) 2 Equation E11 ##EQU00011##
[0162] Where Ir=current rating, N=total number of winding turns, j=winding window, ATj=Ampere-turns in winding window j and Nw=number of winding windows.
I r 2 = B max 2 μ 2 N 2 ( j = 1 Nw ( H w ( 1 ± α ) + 2 R Ij ln ( R oj R Ij ) ) ) 2 Equation E12 ##EQU00012##
[0163] Where Ir=current rating, Bmax=maximum flux density, μ=permeability of core material, N=total number of winding turns, Nw=number of winding windows, Hw=thickness of the winding, α=uniformity factor, j=winding window, RIj=inner radius of winding window j and ROj=outer radius of winding window j.
L = 2 E I r 2 Equation E13 ##EQU00013##
[0164] Where L=inductance of inductor, E=energy stored in core and Ir=current rating.
L = μ N 2 ( 1 + α 2 ) 2 π ( R c 2 H c - H w 1 N w R Oj 2 - R Ij 2 ) [ j = 1 N w ( H w ( 1 ± α ) + 2 R Ij ln ( R Oj R Ij ) ) ] 2 Equation E14 ##EQU00014##
where L=inductance of inductor, Hc=core height, Hw=winding thickness, μ=permeability of core material, Bmax=maximum flux density, α=uniformity factor, j=winding window, ROj=outer radius of winding window j, RIj=inner radius of winding window j, Nw=number of winding windows, Rc=outer radius of core and N=total number of winding turns.
[0165] The ideal DC resistance Rdc is obtained from equation E15.
R dc = ρ cu 2 π H w ln ( 1 / α ) j = 1 N w n j 2 Equation E15 ##EQU00015##
where ρcu=copper resistivity, Hw=thickness of the winding, α=uniformity factor, j=winding window, Nw=number of winding windows, nj=number of turns in winding window j and Rdc=DC resistance of inductor.
[0166] Based on the number of turns calculated from equation E8, each winding window can be divided into different number of turns. FIG. 15 depicts an example of dividing the winding window j (with radius RIj and ROj) into eight turns, with spacing of I and d between the turns horizontally and vertically. The values of I and d depends on the winding configuration and fabrication clearance. Assume the total clearance is ml horizontally and nd vertically, then the effective radius becomes equation E16 where m=the number of clearance spacing on the horizontal direction, n=the number of clearance spacing on the vertical direction.
R Ij ' = R Ij + ml 2 R oj ' = R oj - ml 2 Equation E16 ##EQU00016##
[0167] Where RIj=inner radius of winding window j and ROj=outer radius of winding window j.
[0168] The effective factor α is calculated as in equation E17.
α j = R Ij ' R oj ' = R Ij + ml / 2 R oj - ml / 2 Equation E17 ##EQU00017##
[0169] Where RIj=inner radius of winding window j and ROj=outer radius of winding window j.
[0170] The effective winding thickness of winding window j becomes equation E18.
Hw--.sub.e=Hw-nd Equation E18:
[0171] Where Hw--.sub.e=effective winding thickness and Hw=winding thickness.
[0172] Therefore, equation E15 can be modified to calculate the practical resistance as shown in equation E19:
R dc ≈ ρ cu 2 π H w _ e j = 1 N w ( n j 2 ln ( 1 / α j ) ) Equation E19 ##EQU00018##
[0173] Referring back to equation E1, the time constant T can then be calculated where L and Rdc can be found in equations E14 and E15. In order to validate the concept of balanced field inductor, various ways of fabrication for the core and the winding were explored, including the routing process, laser process on the core, etching technique on copper, and screen printing with silver paste. The most successful results were obtained from the routing process on both the core and the winding. In one embodiment, a Micrometals® core having a relative permeability of about 22 and a winding made of copper sheets of about 0.5 mm thick are used. The fabricated inductor prototype shows a significant improvement in energy density: at the same inductance and resistance, the volume of the balanced field inductor is about two times smaller than that of comparable a conventional inductor.
[0174] FIG. 8 is a flowchart depicting the steps by which the enclosed core type of the present inductor is configured. The electrical inputs to the design include target inductance Lo, rated current Ir, and target DC resistance Ro. The magnetic inputs include maximum magnetic flux density Bmax and permeability μ. The mechanical inputs include the footprint radius Rc and inductor height Hc. The uniformity factor α is swept and all design variables are calculated until the required or desired inductance Lo and dc resistance Ro are met. Step 36 shows the first step where the uniformity factor α is initialized to be 0.5, which is the minimal value to maintain the benefit of a balanced field. Then in step 54, the plate thickness Hp, radius RO1, RI1, and RO2 can be calculated by solving Equations E2, E4 and E5 simultaneously. After Hp has been determined, the radii of the remaining winding windows can be obtained recursively as shown in step 56. It shall be noted that the total number of winding windows Nw is limited by the manufacturing constraints such as the width of the winding and the distance between the winding and the center of the core. The number of turns nj is then determined as shown in step 58 before the inductance L and resistance Rdc are determined from Equations E13 and E15 as shown in step 60. If the requirements cannot be met or if the inductance is not greater or equal to the desired inductance Lo and the resistance is not less than or equal to the desired resistance Ro, the uniformity factor α is increased as in step 46 and the process is repeated. If no uniformity factor α gives a satisfied inductance and resistance, increase the dimension of the core Rc and/or Hc and repeat the procedure. If the calculated inductance and resistance are both better than the target, the inductor volume can be further reduced.
[0175] Enclosed Core Inductor
[0176] FIG. 9 is a top view of an inductor 2 according to one embodiment of the present inductor, depicting the inductor without windings. FIG. 10 is a side partially transparent view of an inductor 2 according to one embodiment of the present inductor, depicting the inductor without windings. Three cores, i.e., a first core 4, a second core 6 nested in the first core 4 and a third core 8 nested in the second core 6 are provided. Each core 4, 6, 8 is a toroid where the toroid annular shape is substantially defined by an object generated by revolving a plane geometrical figure about an axis external to that figure which is parallel to the plane of the figure and does not intersect the figure. In one embodiment, the cross-sectional shape of each exposed end of each toroid if dissected with a plane coplanar to the central axis of each toroid, is a circle. In another embodiment, such shape is a rectangle. Each core is separated from its adjacent core with a slotwidth 10. For ease of ensuing discussions, for enclosed core inductors, j, RIj and ROj are defined as the referenced core, the inner radius of core j and the outer radius of core j, respectively. Note that, instead of referencing a winding window as in the case of an enclosed winding inductor, j now references a core. Again, each core is constructed from a magnetically permeable material.
[0177] FIG. 11 is a top view of an inductor 2 according to one embodiment of the present inductor, depicting the inductor with windings. FIG. 12 is a top view of an inductor according to one embodiment of the present inductor, depicting the windings through various cores with portions of the winding removed to reveal only the portions disposed through slotwidths and over the outer radius of the first core 4. In this embodiment, the winding is applied to and encompassing all three cores 4, 6, 8. In doing so, note that some winding portions 18 are wrapped around the first core 4 only, some winding portions 20 are wrapped around the first and second cores 4, 6 and yet some windings 22 around all three cores 4, 6, 8.
[0178] FIG. 13 is a flowchart depicting the steps by which the enclosed core type of the present inductor is configured. First, the uniformity factor α is initialized at 0.5, which is the minimal value to maintain the benefit of a balanced field as shown in step 36. The geometrical parameters of the cores, e.g., the footprint radius and thickness of a core are determined. Based on the uniformity factor α initialized in step 36, the outer radius ROj of core j and the inner radius RIj of the core j are determined as in step 38 from equation E21. The ampere-turns is then determined as in step 40 using equation E20. The ampere-turns (NI) between ROj and RO(j+1) is determined using equation E20:
NI=αjHmax2π(Roj-Ro(j+1)) Equation E20:
[0179] Where j=core, ROj=outer radius of the core j, RO(j+1)=outer radius of the core inside of the core (j+1), NI=ampere-turns, N=number of turns of core j, I=current rating, αj=uniformity factor of core j and Hmax=maximum magnetic field. The magnetic field reaches its maximum value at the inner radius RIj of a core j.
[0180] The stored energy E, inductance L and resistance Rdc of the core can then be calculated as in step 42. If the E, L and Rdc of the core do not meet desired values as determined in step 44, the uniformity factor α is increased and this iterative process continues until the calculated E, L and Rdc meet the desired values where Lo is the desired inductance and Ro is the desired resistance.
ROj/RIj=1/α Equation E21:
[0181] Where j=core, ROj=outer radius of core j, RIj=inner radius of core j and α=uniformity factor.
[0182] Inductance L is calculated as in Equation E22.
L = j = 1 ncell μ * h 2 π * [ N j 2 * ln ( R j max R j min ) ] Equation E22 ##EQU00019##
[0183] Where j=core, h=core height, ncell=total number of cores, Nj=total number of turns enclosed by cell j, Rjmax=outer radius of core j, Rjmin=inner radius of core j and μ=permeability of core material.
[0184] Resistance Rdc is calculated as in Equation E23:
Rdc=(ρ*length)/area Equation 23:
[0185] Where ρ=resistivity of winding, length=total length of winding, area=cross-sectional area of winding=width*thickness, where width=(2*π*Rncellmin)/Nncell, Nncell=Number of turns enclosing ncell and Rncellmin=inner radius of ncell.
[0186] As the uniformity factor α represents the uniformity level throughout the magnetic field in a balanced field design, a relatively large uniformity factor is always preferred. For a given volume, an optimal uniformity factor always exists that gives the highest time constant. The optimal value of uniformity factor varies with different situations and input parameters such as the footprint and height of the inductor. However, the uniformity factor cannot always be ideally selected as it is usually limited by the fabrication constraints. The plate thickness, for example, which is defined as Hp and calculated from equations E2-E6, decreases as a increases since thinner plates are needed to increase the flux density. The plate thickness for each core is minimized as much as possible but within fabrication limitations. Therefore, the uniformity factor can only be as close to unity as fabrication limitations permit.
[0187] To further generalize the aforementioned inductor design methods to broaden the spectrum of applications, a normalization method based on radius Rc, or the like, can be applied. For example, the required inductance, volume, and resistance are given as inputs to the design procedure described elsewhere herein, and the winding distributions are design outputs that ensure balanced field inside the core. To make the design procedure for both types of inductors (enclosed-core and enclosed-winding) more generalized and applicable to a wide range of dimensions, all the geometrical factors can be normalized to the footprint radius Rc so that they become dimensionless. The design output can be scaled up or down to the desired values.
[0188] The detailed description refers to the accompanying drawings that show, by way of illustration, specific aspects and embodiments in which the present disclosed embodiments may be practiced. These embodiments are described in sufficient detail to enable those skilled in the art to practice aspects of the present invention. Other embodiments may be utilized, and changes may be made without departing from the scope of the disclosed embodiments. The various embodiments can be combined with one or more other embodiments to form new embodiments. The detailed description is, therefore, not to be taken in a limiting sense, and the scope of the present invention is defined only by the appended claims, with the full scope of equivalents to which they may be entitled. It will be appreciated by those of ordinary skill in the art that any arrangement that is calculated to achieve the same purpose may be substituted for the specific embodiments shown. This application is intended to cover any adaptations or variations of embodiments of the present invention. It is to be understood that the above description is intended to be illustrative, and not restrictive, and that the phraseology or terminology employed herein is for the purpose of description and not of limitation. Combinations of the above embodiments and other embodiments will be apparent to those of skill in the art upon studying the above description. The scope of the present disclosed embodiments includes any other applications in which embodiments of the above structures and fabrication methods are used. The scope of the embodiments should be determined with reference to the appended claims, along with the full scope of equivalents to which such claims are entitled.
User Contributions:
Comment about this patent or add new information about this topic:
| People who visited this patent also read: | |
| Patent application number | Title |
|---|---|
| 20220290385 | CONTRAST ROAD MARKING APPARATUS |
| 20220290384 | Self-propelled construction machine or mining machine |
| 20220290383 | METHOD OF PAVING A ROAD SURFACE AND ASPHALT PAVING SYSTEM |
| 20220290382 | ROAD FINISHING MACHINE WITH LEVELING CASCADE CONTROL |
| 20220290381 | ROAD FINISHING MACHINE WITH SUCTION DEVICE |